
Graph Efficient Frontier In Excel How To Create Expected
Now, I want to graph the efficient frontier line - ie, the minimum standard deviation possible at any given expected return level.Hi, im trying to plot the Markowitz efficient frontier in Excel. The point of tangency is the most efficient portfolio.Hi guys, I've figured out how to create expected returns and standard deviations for a portfolio of assets at any given percentages. If we draw a line from the risk-free rate of return, which is tangential to the efficient frontier, we get the Capital Market Line. Read more represents combinations of risky assets. This frontier is formed by plotting the expected return on the y-axis and the standard deviation on the x-axis.
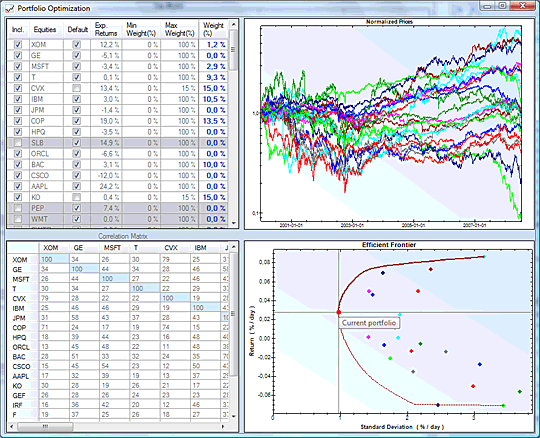
All of the correlations are off screen, as is part of the data that drives the portfolio return/stdev, but those should be irrelevant to what I'm trying to do.Okay - so the problem is to run solver to minimize SD while attaining a stipulated minimum return, then run it agains for another stipulated return, etc. I think the macro should input the resulting risks and returns in a table anywhere below that.I just have no experience with VBA and macros, so I could use some help in the actual building of the code.EDIT: Here is the code for a small section of what i'm working with. Total portfolio standard dev in cell G19. Total portfolio expected reutn in cell G18.
Obviously you will have to adjust the starting minimum yield and increment according to your needs.Edited for typos and (I hope) clarity - Oct 25You already calculate the expected yield for a given asset allocation in G18 we want a calculation of G18 - the value in MinYield let's assume that this value is in cell G20. I would also keep the weights for each asset class, by transposing them into the cells to the right of the expected yields and SDs - but that is a personal preference. = + 0.005 ' increments required return by 0.5%SolverSolve userfinish:=True ' runs solver, returns results w/o dialogueSolverfinish keepfinal:=1 ' tells solver to retain final values in.offset(i,0) = range("G18").value ' pastes expected portfolio yield.offset(i,1) = range("G19").value ' pastes expected portfolio SDYou can add headings if you like, and I would probably add a column with the minimum stipulated yield, just in case it is very low, and any portfolio will provide it - ie, if the lowest asset return is greater than the minimum required yield. I assume that the cell with the stipulated return in it is called MinYield. I prefer this method - the fewer times you are buggering around with Solver, the better.The code to do this (warning Air Code) would look something like this, assuming that you set a named range ("Result") in the s/sheet (roughly around D25) where you want the results to appear. You would then set a solver constraint that this value be >=0, and change the minimum required return on the s/sheet for each iteration of solver.
Under that box, click the "Min" radio button - this tells Solver that you want to minimize the value in G19 - the SD of expected portfolio yields> Click in the "By Changing Cells" drop down, and enter G3:G15 - again, you can either type it or point and click, and I think Solver makes it an absolute reference. Similarly is short for Range("Result").Setting up Solver (only required once, unless you change your model)> Click on Tools | Solver - this will bring up the Solver dialogue box, with a title "Solver Parameters"> Click in the "Set Target Cell" drop down, and either enter G19 (IIRC, solver will make it an absolute reference by default) or click and point to it on the s/sheet. The two approaches are equivalent - I just find writing code to manipulate the Solver a little kludgy if I recall correctly, it needs the contraint fed in as a string - bleh.In VBA, the square brackets are a short form for the "evaluate" function - anything inside square brackets is evaluated - in this case, since it is a named range inside the brackets it is a short form for range("minyield') - I just find the square brackets less verbose and easier to read.
This tells Solver that possible solutions will only be acceptable if the difference between the expected yield and the stipulated yield are positive or zero. Click Add to include this constraint in the Solver model. The other options in the middle box allow either an "Int(eger)" constraint (the value must be an integer) or "bin(ary)" constraint (I never use it, but IIRC, it is really a boolean constraint, either true or false). The middle dropdown tells Solver whether the cell should be Greater Than, Less Than, or Equal To the value (or cell reference) on the right hand side - in this case select ">=" in the middle and type "0" in the right hand drop down. The left dropdown must be a cell reference - in this case, G20 (or the cell that contains the actual expected yield - the minimum acceptable yield, as discussed above).
You may not need 20 iterations - I was even thinking in the first version that it made more sense to allow that to be user-selectable this just makes it very explicit and you don't have to worry that you missed changing "20" to "15" (or "40") somewhere in the code (been there, done that. I don't know whether you need to do this to save the Solver parameters - but it doesn't hurt, and it gives you a chance to see how the Solver algorithm works with your data and model set-up.After that, you should be able to run the VBA routine - let me know how it goes.ICount = 20 ' adjust as required for smooth graph = worksheetfunction.Min(range("$E$3:$E$15"))DIncr = worksheetfunction.Max(range("$E$3:$E$15")) - = - dIncr ' so first iteration will be at = + dIncr ' increments required returnIf you haven't done this before, you should plot this as an X-Y graph, not a line graph, so the yield scale doesn't get funny increments like 5.056%.


 0 kommentar(er)
0 kommentar(er)
